ThinkBayes 心得筆記 - Chapter 8
Chapter 8 作者介紹了自己實際通勤的案例,並從地鐵班表建立一個數據模型,由月台上的等車人數推測是否應該繼續等待下去,或是轉搭計程車前往目的地。
ThinkBayes Note
Chapter 8 - Observer Bias
The Red Line Problme
Red Line 為美國 Massachusettss 一條連接 Cambridge 到 Boston 的電車路線。在尖峰時間平均每 7 ~ 8 分鐘到達一班車。現在從 Kendall Square 搭車前往 Needham。當尖峰時間到達 kendall Square 時可能有以下狀況
- 等車人數較少,可推測前一班列車剛走因此需要等待 7 分鐘左右。
- 等車人數較多,可推測列車不久將會到達。
- 等車人數過多,可推測列車並沒有準時運行,因此作者會轉搭 Taxi 前往目的地。
要如何從車站中的現在等通勤人數推測下一班車的到來時間,並決定要等待還是轉搭 Taxi?
Model
為了解決問題,作者了假設通勤者到達車站人數的分佈為 Poisson process,λ 為平均每分鐘的到達數量。(雖然有尖峰離峰時間,但觀察時間是在每天相同區段,因此可將 λ 當成常數)。而該路線在尖峰時間約每 7 ~ 8 mins 發一班車,但 Kendall Square 的車輛到達間隔約為 3 ~ 12 mins。
為了研究真正的列車時間,作者從 MBTA官網 處下載得到真正紀錄的列車到到達時間,並取出工作日中 4pm ~ 6pm 的車輛到達時間間隔(連續五天,每天約記錄到 15 班車到達間隔)形成分佈 z。
Observer bias
如果 4pm ~ 6pm 都在車站記錄到達時間,那所得到的結果會與官方資料相同。但觀察者實際上所觀測到的間隔時間可能會比真正的時間來得多。因觀察者更有可能在長區間到達而得出較長的結論。
假設區間有 5 mins 與 10 mins 兩種且發生機率都為 1/2,則平均區間時間為 7.5 mins。但實際上通勤者更可能到達 10 mins 的區間內。假設在 15 mins 內包含一班間隔時間 5 mins 一班 10mins 的車,通勤者有 1/3 的機會到達 5 mins 區間而有 2/3 會到達 10 mins 區間。因此觀察到的區間為 5*(1/3)+10*(2/3) = 8.33。該觀察上的誤差就被稱為 Observer bias。
Observer bias 的情況也常發生在現實生活中,如遇到飛機全滿的搭乘者較多,就會在統計上得到認為飛機全滿的機率比真正狀況更高。
依照先前的討論可建立兩個機率分佈
- 以官方資料建立真正的列車到達區間分佈 z
- 由觀測資料所建立的車輛主觀到達區間分佈 zb (z biased)。
zb 分佈可由 z 分佈計算得出
$$zb = Normalize(P(Z_{time})*Z_{time})$$結果如下
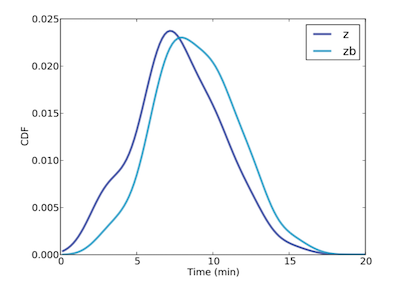 z 與 zb 的分佈圖
z 與 zb 的分佈圖
Wait times
設定兩個數值 x 與 y,其中
- x: 為前一班車到達與 passenger 到達車站的間隔時間 (elapsed time)。
- y: passenger 到達車站與下一班車到達的間隔時間 (waiting time)。
因此 zb 的分佈為 x 分佈與 y 分佈的加總
$$zb=x+y$$現在假設觀察者到達車站時間為 5 mins 區間,則等車時間(waiting time)分佈為 0 ~ 5 mins 的 Uniform distribution。如果為 10 mins 則為 0 ~ 10 mins 的 Uniform distribution。因此等車時間分佈 y 可由 zb 分佈形成的 Mixture of uniform distribution 得出。結果如下
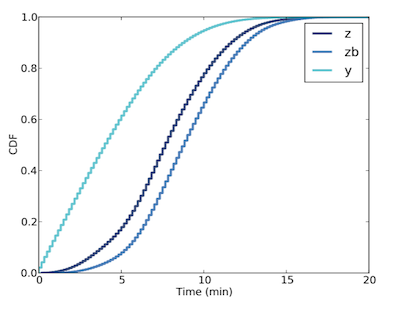 z, zb 與 y 的 CDF
z, zb 與 y 的 CDF
其中
$$z_{mean} = 7.8$$ $$zb_{mean} = 8.8$$ $$y_{mean} = \frac{zb_{mean}}{2} = 4.4$$在統計結果後,尖峰時刻約每 9 mins 發車,接近 zb 的 mean 而不是 z。
作者有寄信去問 MBTA,對方也回信表定時間不一定正確。此外 CDFs 比較好在同一張圖上繪製多個機率分佈,且也比較容易解釋。
Predicting wait time
當乘客現在到達車站後有 10 個人在等車,那該做什麼行動呢? 現假定實際分佈為 z,且 passenger 平均到達人數 λ = 2, y 分佈可由以下步驟計算
- 使用公開資料建立真正分佈 zp 的 Prior 分佈 z。
- 用通勤者數量來計算 x (elapsed time) 分佈。
- 使用 $$y = zp - x$$ 的關係式,來計算 y (waiting time) 分佈。
相關方式已在前面太探討過,結果如下圖
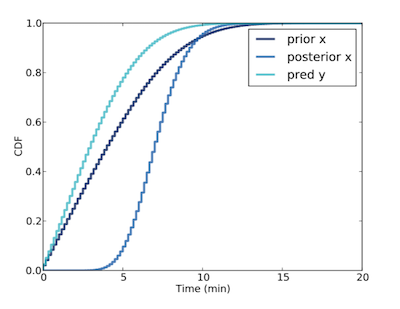
可知上一班車最有可能離開 5 ~ 10 mins,因此我們可以預測下一班車到達時間約有 80% 的可能性少於 5 mins。
Estimating the arrival rate
之前在做預測時作者給了兩個假設
- 已知的到達時間間隔分佈。
- 通勤者到達率。
現在作者放鬆第二個假設,先記錄一個星期的實際的到達車站時的等待人數(k1),等待時間(y),以及等待時到達的人數(k2),結果如下
| k1 | y | k2 |
|---|---|---|
| 17 | 4.6 | 9 |
| 22 | 1.0 | 0 |
| 23 | 1.4 | 4 |
| 18 | 5.4 | 12 |
| 4 | 5.8 | 11 |
可得出這星期平均總等待時間(y)為 18,而等待時的到達總人數為 36,通勤者到達率為每分鐘 2 人。在這邊作者將到平均到達人數 λ 設為 Hypothesis,Likelihood 為等待時間與等待時到達人數的 Possion 分佈,計算後得到以下分佈
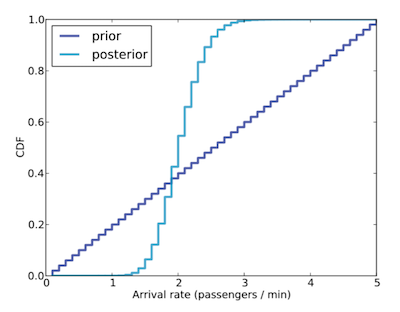
可看到 Posterior 的平均數和中位數區域都非常接近觀測到的結果 - 每分鐘 2 人。但因我們的 sample 數量太小,因此實際的 Posterior
Incorporating uncertainty
當存在非確定數值的輸入時,我們可以使用以下方式
- 先分析非確定數值(本範例為 λ)。
- 計算非確定參數的分佈。
- 分析每個參數的數值並建立預測分佈的集合。
- 使用參數的權重分佈,計算預測分布的 Mixture distribution。
以此範例來說,前一部分已分析 Hypothesis λ 並得到該參數的分佈,之後可用該分佈的 mixture distribution 建立等待時間的機率分佈,如下圖
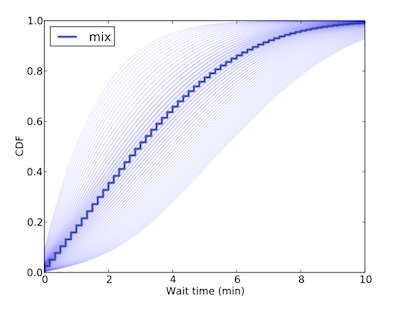
背景中較淡的陰影線為不同 λ 所建立的等待時間分佈,而中間的深色線為所有分佈建立的 Mixture distribution。
Decision analysis
在前面分析了堆事情,但還沒做最後一件事 - 決定接下來的行動是要等車還是離開車站轉搭計程車。在這邊可以使用到達車站時等車人數來預測接下來的等待時間,假如個超過一定時間(設為 15 分鐘)就轉搭計程車。作者先依照過去一整年的資料建立分佈,並加入了 Long delay 資料後得出以下結果
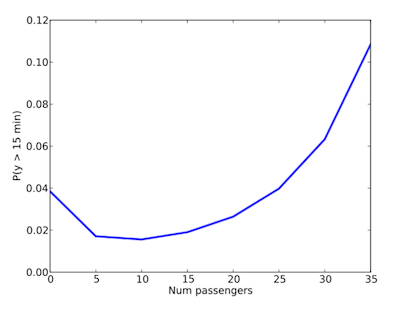
根據分佈可知當等車人數少於 20 人時可推測系統運作正常,long delay 機率很低,而當超過 30 人時我們可以推測距離上一車已經超過 15 mins,超過一般的行車間距,可能是發生嚴重誤點問題。因此作者的結論為當等車人數少於 30 人時,應該在原地繼續等車,超過 30 人則轉搭計程車。
