Isomap - Isometric Mapping
Isomap,全名為Isometric Mapping, 是一種基於Classical MDS所產生的非線性降維演算法(Nonlinear Dimensional Reduction)。 一般來說,如果資料有著線性分佈的性質,如PCA與MDS這類計算整體資料(Global)之間的關係後再進行降維的線性演算法, 都會有不錯的效果。但如果資料本身為非線性分佈,古典PCA與MDS則時常無法在降維後正確展現出資料間的關係。
如下圖資料分佈呈現螺旋狀,被稱為瑞士卷(Swiss Roll)的資料型態,
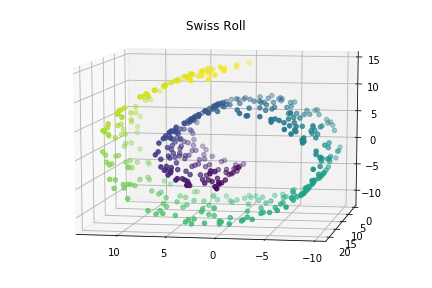
使用PCA對該資料集進行降維後可得到下圖的結果。
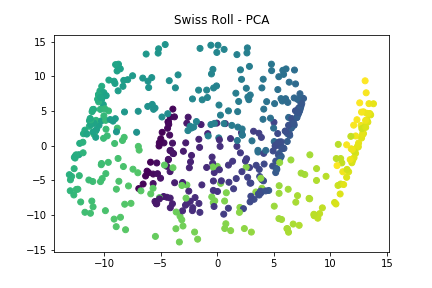
可以看出降到二維後,並沒有正確表現出資料的分佈狀態。而使用MDS進行降維,也產生同樣的問題。
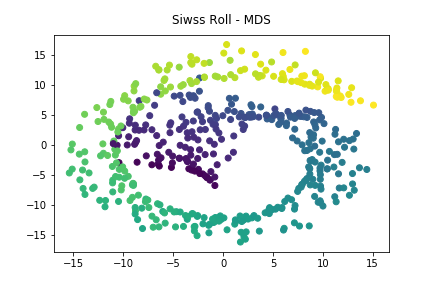
主要因為PCA與MDS演算法所考慮到的是Global資料分佈,沒有辦法處理像Swiss Roll這樣螺旋分佈的非線性資料狀態。 因此我們可以知道,資料分佈特性對降維演算法效果有著非常大的影響。
Isomap(Isometric Mapping,等距特徵映射)
Isomap為 J. B. Tenenbaum,V. de Silva與J. C. Langford在2000年時提出的一種基於MDS與Manifold的降維演算法。 Manifold在幾何學上,指的是局部具有歐式空間性質的空間。一個例子就是地球表面。球面本身是非歐幾何,即從赤道上的延伸兩條平行線,在一般的歐式空間中平行線並不會相交,但因空間本身是彎曲的,因此平行線會在極點交會(如經度線)。雖然在大尺度(Global)中球面為非歐幾何,但世界地圖卻能由一群由歐式幾何平面二維地圖所組合而成。因此球面可以說是一個二維Manifold。
將這個想法應用到MDS演算法時,可以將資料實際分佈與距離看成是可由局部建立出整體的Manifold結構。
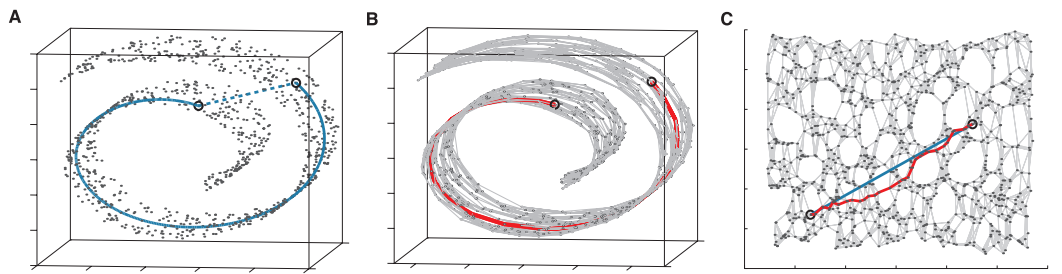
**圖(A)**顯示在Swiss roll data set中,兩點的實際距離並非藍色虛線所表示的的高維歐式距離,而是的低維度上的藍色實線(Geodesic distance)。**圖(B)**中的紅線爲以Neighborhood Graph所建立出來的兩點間最短路徑。**圖(C)**為用Isomap降到二維後,兩點間的歐式距離(藍線)與Shortest Path路徑(紅線)的差異。
Algorithm
-
依照K個最近的點(K nearest neighbors)或是一定距離內的點(some fixed radius), 定義每點的Neighbor。
-
依照前一步的neighbor關係,依照歐式距離建立所有點的Neighborhood Graph。
-
使用Dijkstra或Floyd–Warshall等最短路徑(Shortest Path)演算法,依照建立出的Neighborhood Graph,計算每點之間的最短距離。
-
以Shortest Path建立出來的距離矩陣,執行**MDS(Multidimensional Scaling)**演算法降維。
Code
以下使用Scikit-learn中的Isoamp元件示範
# 匯入相關Package
import matplotlib.pyplot as plt
from sklearn import datasets, manifold
from mpl_toolkits.mplot3d import Axes3D
from sklearn.manifold import Isomap
# 產生 Swiss Roll data set
swiss_roll_data = datasets.make_swiss_roll(n_samples=500, random_state=0)
data = swiss_roll_data[0]
rel = swiss_roll_data[1]
## 位置顯示原始資料分佈
fig = plt.figure()
ax = Axes3D(fig=fig)
ax.scatter(xs=data[:,0], ys=data[:,1], zs=data[:,2], c=rel)
ax.view_init(azim=100, elev=10)
# 建立 k = 8 的 Isomap Model並將資料
isomap_model = Isomap(n_components=2, n_neighbors=8)
isomap_result = isomap_model.fit_transform(data)
plt.scatter(x=isomap_result[:, 0], y=isomap_result[:, 1], c=rel)
在K=8時的降維結果如下,
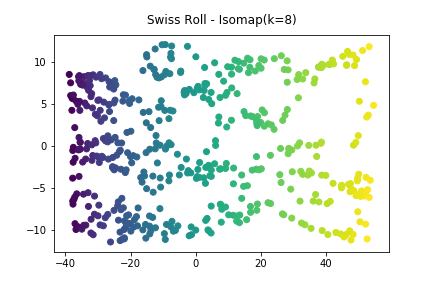
可看出原本Swiss Roll資料集,被攤開成二維平面,並沒有向之前的PCA或MDS一樣使資料混在一起, 在降維到2D後仍保有原先資料分佈關係。
Issue
由於Isomap是由每點之間的Neighbors來建立出整個連結距離網路,因此鄰近點數量會大幅影響到降維結構。 若是太少會無法使結構無法正確展現,太多則會有可能產生Shortcut狀況,下圖為使用
$$K=3$$以及
$$K=15$$時的降維結果
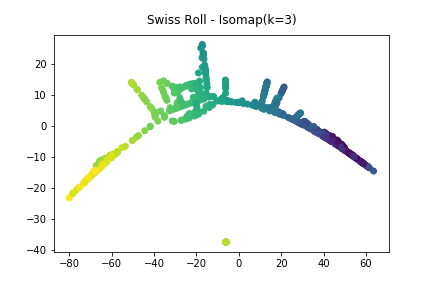
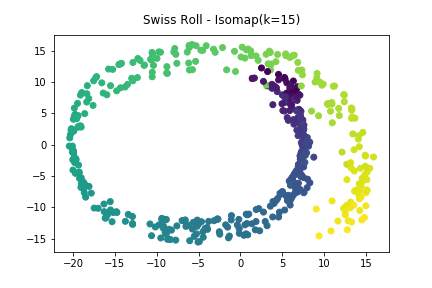
可看出在鄰近點過多過少的,都會使降維結果受到影響,因此在使用Isomap時需要測試不同的Neighbor參數, 已找到最佳降維的參數與結果。
